DAY 5 – DAW January

Rigid body; Degrees of freedom, Euler’s theorem, angular velocity, angular momentum, moments of inertia, theorems of parallel and perpendicular axes,

Questions:

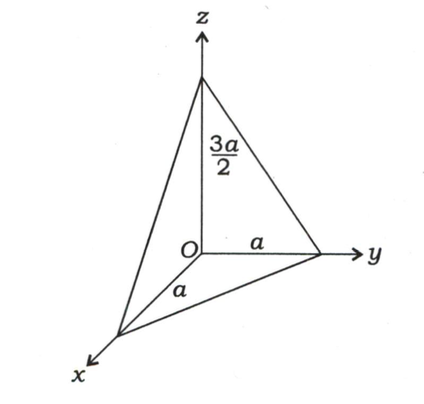
Q 1. A homogeneous right triangular pyramid wih the base side $a$ and height $\frac32a$ is shown below. Obtain the moment of inertia tensor of the pyramid. [15 marks]

Q 2. The angular momentum $\vec M$  of a rigid body comprising of N particles and rotating with angular velocity  $\vec \omega$ is given by $\vec M = \displaystyle\sum_{k=1}^N m_k \vec r_k \times (\vec \omega \times \vec {r_k})$  , where the origin coincides with the centre of mass. Express the components of $\vec M$  in terms of components of the inertia tensor. Hence, show that the most general free rotation of a spherical top is a uniform rotation about an axis fixed in space. [15 marks]

Video Solution: